AVL Tree

Introduction to AVL Tree

----------------------------------------------------------------------

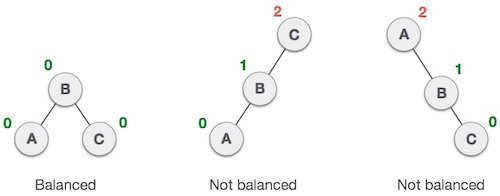
AVL Tree is a variation of Binary Search Tree that performs self-balancing so that the height difference between the right and left subtrees is no more than one. The advantage of having a balanced Binary Tree is having a better worst-case search speed compared to a regular Binary Search Tree. AVL Tree guarantees that the search speed will always be at O(log n).

Example of what constitutes as an AVL Tree, and what doesn't:

In AVL Trees, Balance Factor refers to the height difference between the right and left subtrees. An AVL Tree may have a Balance Factor of 1, -1, or 0 to be acknowledged as an AVL Tree.

Insertion

----------------------------------------------------------------------

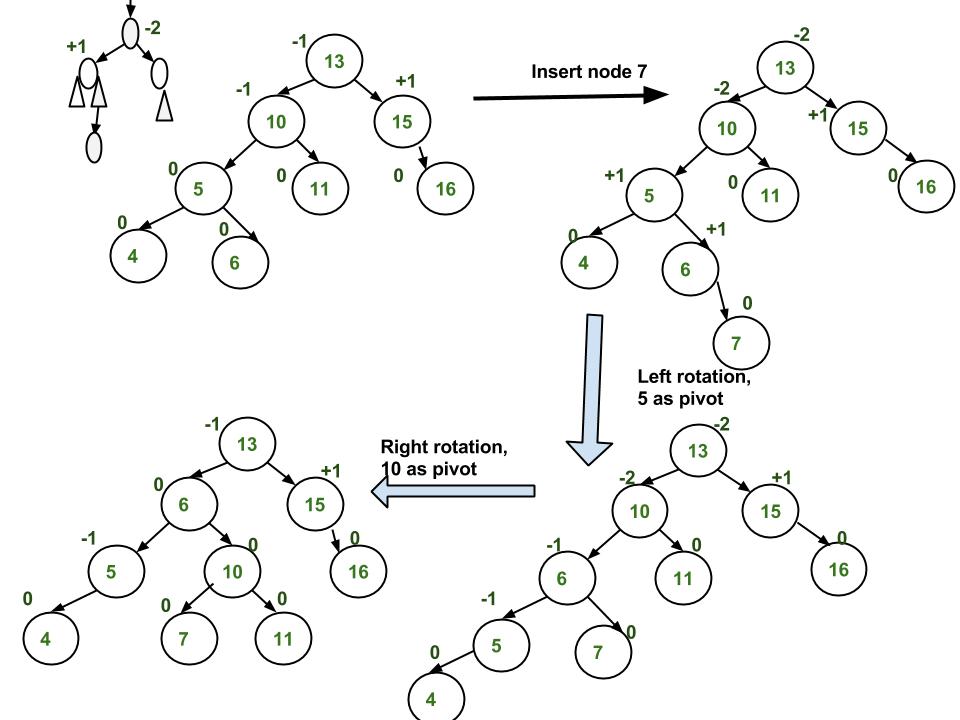
AVL Trees has an insertion operation like normal Binary Search Trees. However, AVL Tree checks whether the balance factor of the tree is 1, -1, or 0. If not, then it will perform rebalancing. There are four main ways to rebalance a tree, known as Left Rotation, Right Rotation, Left-Right Rotation, or Right-Left Rotation.

Insertion - Single Rotation

----------------------------------------------------------------------

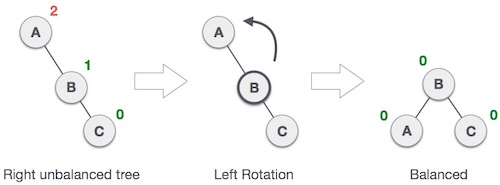
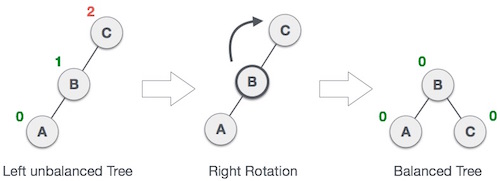
Single Rotation is a term that refers to Left Rotation and Right Rotation. It means that rebalancing the tree will only take one rotation. Left Rotation is used when the imbalance is in the left subtree, and Right Rotation is used when the imbalance is in the right subtree. Single Rotation is performed when the opposing subtree follows a straight path (left-left or right-right)

Examples of Left and Right Rotation:

Insertion - Double Rotation

----------------------------------------------------------------------

Double Rotation is a term that refers to Left-Right Rotation and Right-Left Rotation. Double Rotation is performed when the imbalance requires two rotations to be fixed. Double Rotation is performed when the opposing subtree has a zig-zag shaped path (left-right path or right-left path).

Left-Right Rotation occurs when the problem is in the right subtree of the left subtree, like so:
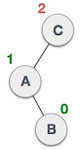 (From C, it goes a left->right path towards B)

On the other hand, Right-Left Rotation occurs when the problem is in the left subtree of the right subtree, like so:
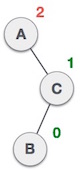 (From A, it goes a right->left path towards B)

A Double Rotation problem can be visualized as such:

What happens in both cases is that single rotation occurs two times on the "pivot".

Deletion

----------------------------------------------------------------------

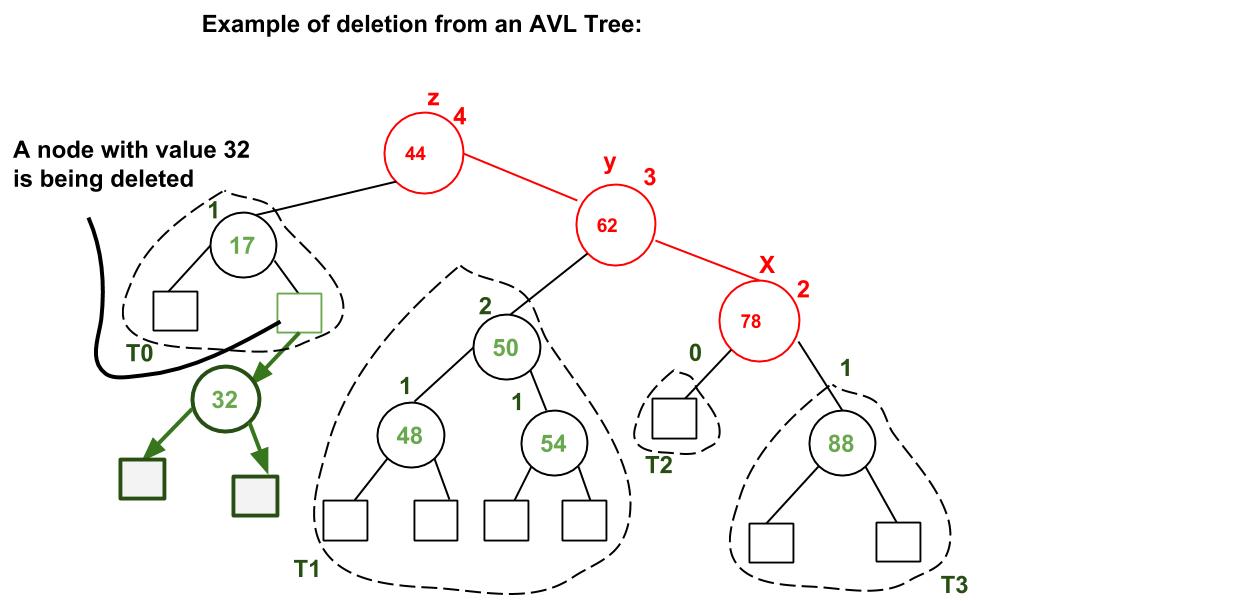
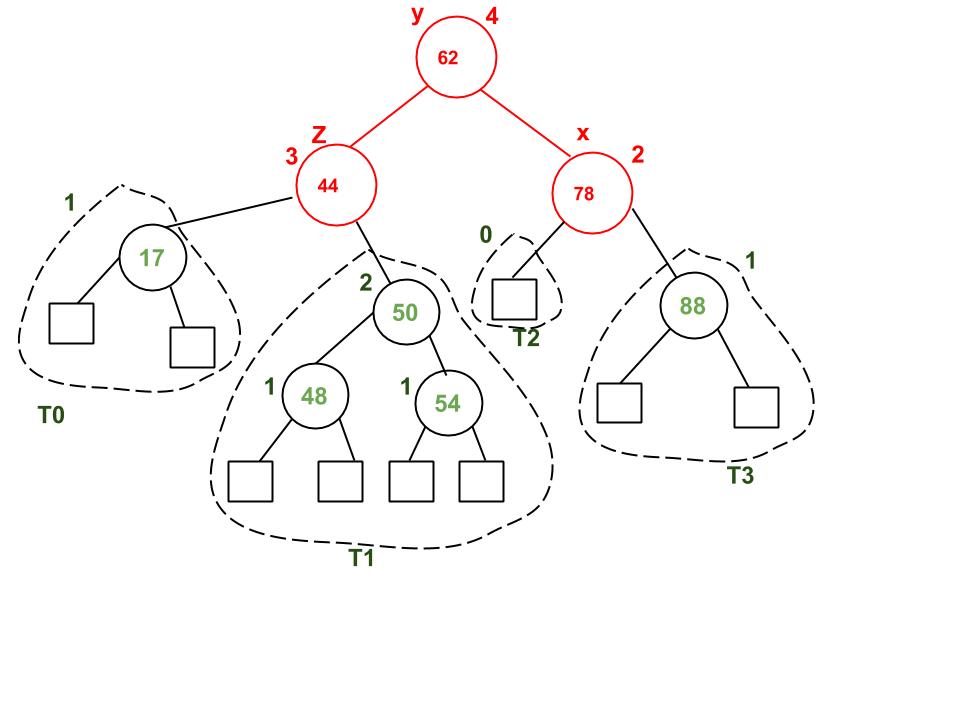
Like with Insertion, Deletion in AVL Tree is just like Deletion in a regular Binary Search Tree, and then it checks if the tree has any imbalance on it. If the balance factor after deleting a node is not 1, -1 or 0, then it will perform one of the four rotations. The main difference with AVL Tree Insertion is that after performing a rotation, it will continue to check whether an imbalance has occured on the ancestors of the rotated node.

Example of AVL Tree Deletion:

Closing

----------------------------------------------------------------------

Thanks for having read this article to the end!

References:
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm
https://www.w3schools.in/data-structures-tutorial/avl-trees/