Heaps and Tries

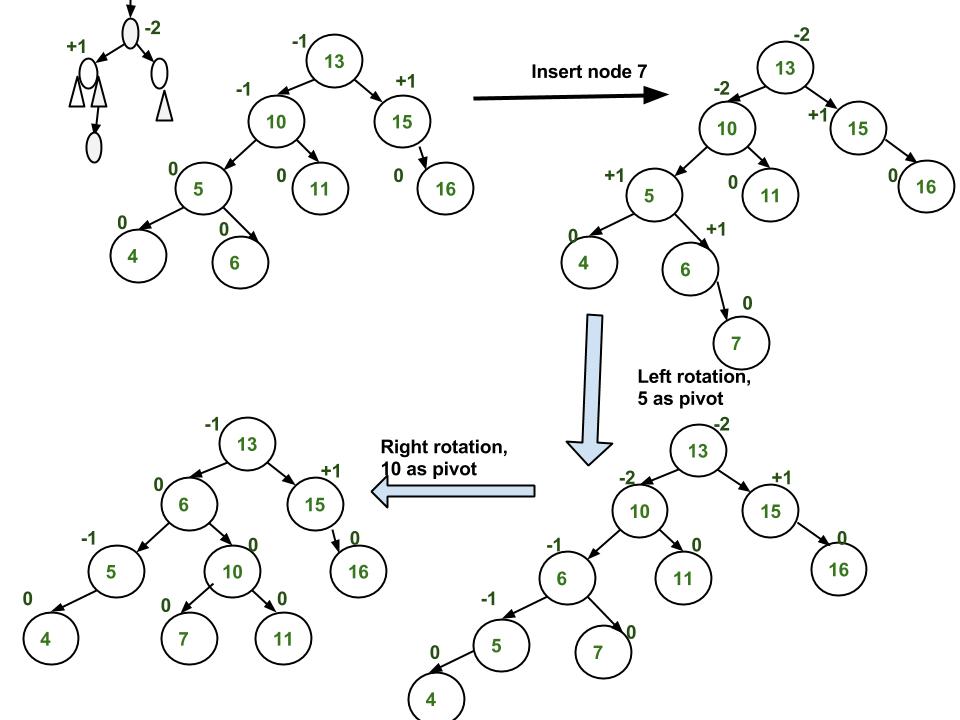
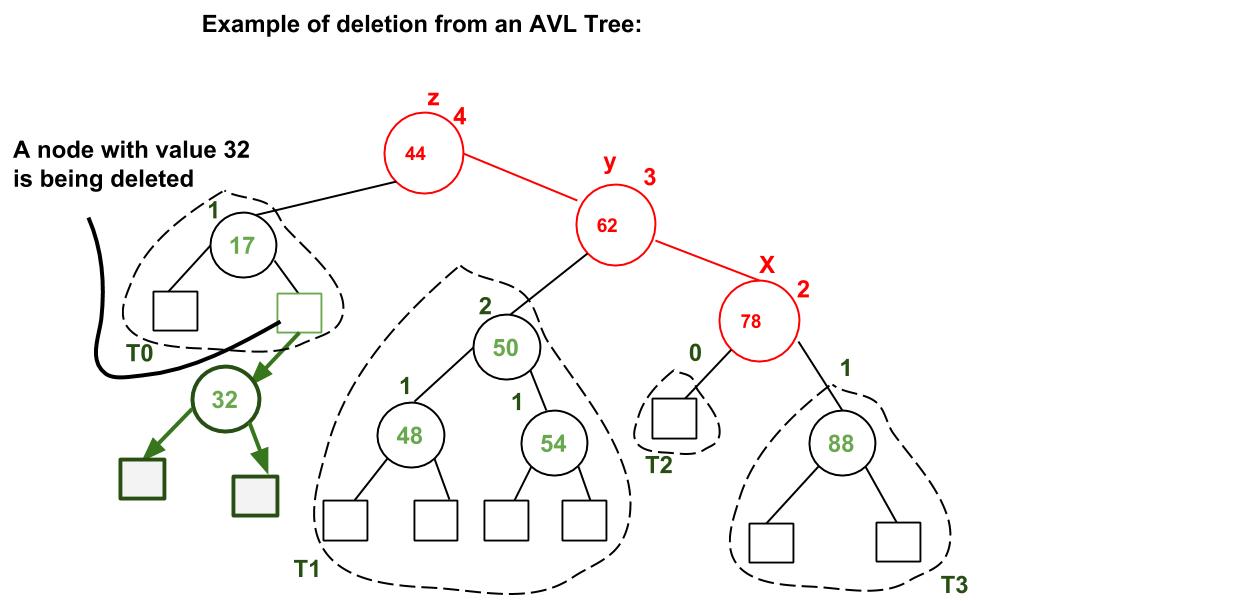
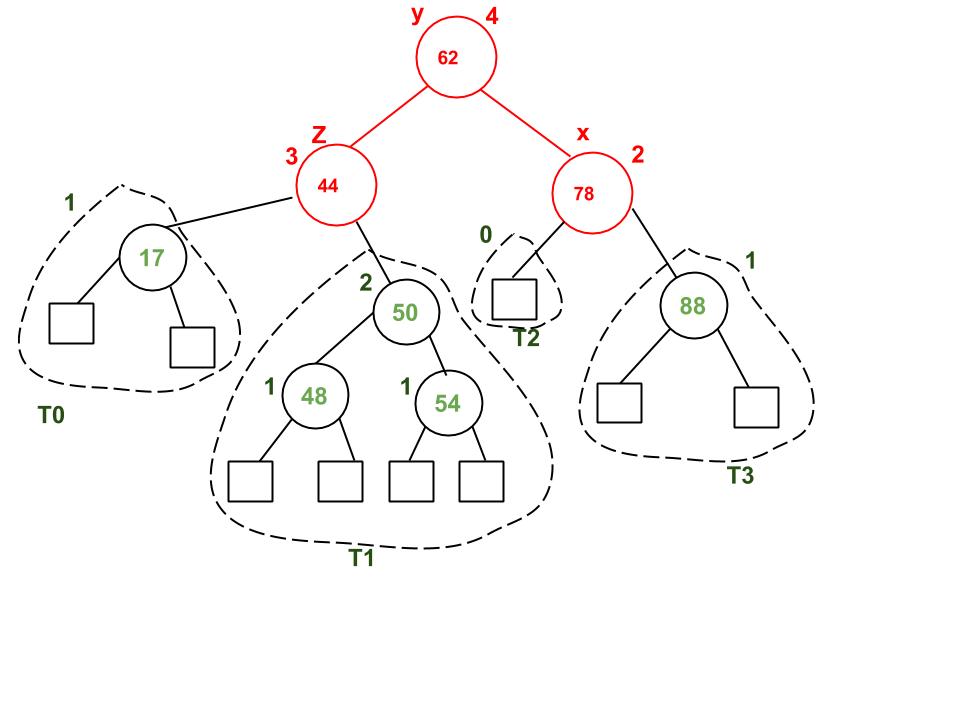
Introduction to Heaps

----------------------------------------------------------------------

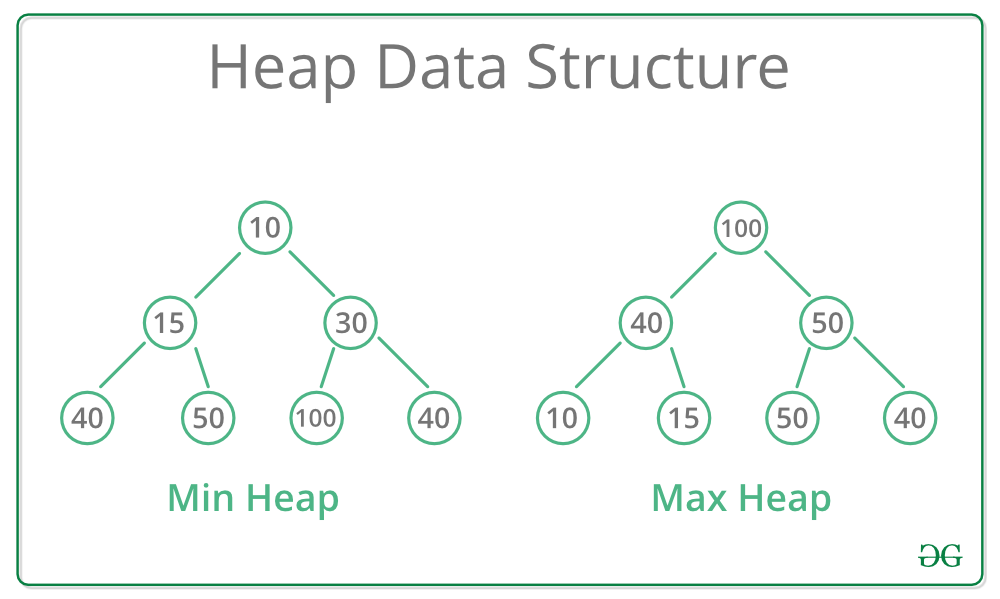
A Heap is a type of tree-based Data Structure where the Heap is always a Complete Binary Tree. Heaps are commonly used to perform Heapsort or to create Priority Queues and Graph algorithms. Heaps also have a time complexity of O(n).

Heaps are often implemented in two types; Min-Heap and Max-Heap. A Min-Heap is when the root node, or parent node during recursion, has the minimum key value for all the keys at all of its children. Max-Heap is when the root or parent node has the maximum key value instead of minimum.

Example of a Min-Heap and Max-Heap:

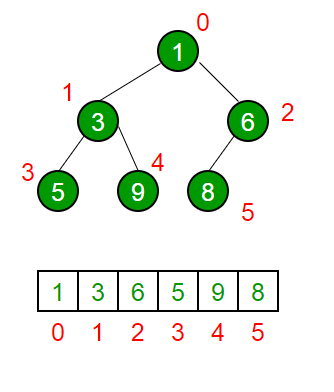
 A Heap is often implemented using Arrays. The root node will always be at Arr[0], while non-root parent nodes is located at Arr[(i-1)/2]. The left child node is located at Arr[(i*2)+1], while the right child node is located at Arr[(i*2)+2]. The traversal method used in array implementation is level order.

Visual example of Heap (Min-Heap) Implementation using Arrays:

Operations on Heaps

----------------------------------------------------------------------

Heaps have a number of functions to use. The most basic of them include:

• getMin(); or getMax(); to return the root value of a Min-Heap or Max-Heap.
• Upheap refers to the process of comparing a key node with its parent node. If the key node is smaller (Min-Heap) or larger (Max-Heap) than the parent node, then the two nodes will switch places to fit with the rules of a Min-Heap or Max-Heap.
• Downheap refers to the process of comparing a key node with its children. If the key node is larger (Min-Heap) or smaller (Max-Heap) than one of its two children, then the key node and the child node will switch places.
• insert(); in Heap is done by adding the key at the end of the tree, then performing upheap recursively to ensure that the tree doesn't have any new violation.
• delete(); in Heap is used to remove the a key from Heap. The deleted node is then replaced with the last node of the tree, and the root performs downheap recursively to ensure that the tree doesn't have any new violation.

Min-Max Heap

----------------------------------------------------------------------

A Min-Max Heap is a Heap where each level alternates between Min-Heap and Max-Heap rules. Min-Levels are located at even levels (Height of 0, 2, 4, etc) while Max-Levels are located at odd levels (Height of 1, 3, 5, etc).

Visual example of a Min-Max Heap:

The root on a Min-Max Heap will have the minimum value of all its nodes. On Min-Levels, the nodes will have the smallest value among its children, while on Max-Levels, the nodes will have the largest value among its children.

A Max-Min Heap is defined as opposite to Min-Max Heap, where the root contains the maximum value in the Heap, and Min-Levels now located at odd levels while Max-Levels are now located at even levels.

Introduction to Tries

----------------------------------------------------------------------

Trie is a tree-like Data Structure where the nodes store letters of the alphabet. With Trie, words and strings can be retrieved by traversing down a Trie. The word "Trie" itself comes from "ReTrieval". Examples of Tries Application are word prediction and spell checkers. Tries are known to have short search time, but relatively large memory usage. Trie is also known as a "Prefix Tree".

The root node of a Trie is always empty, and every node in Tries has an "End of Word" variable, usually in boolean or integer, to determine whether the node is the final letter in the word or string. Tries are implemented in a way not too different from Linked Lists.

Example of a Trie:

Tries - Insertion

----------------------------------------------------------------------

In Trie, the insertion key is a word, and insertion works by checking whether or not the prefix of the key already exists or not. If it doesn't exist, then it creates a new node from the current line of prefixes. If the key already exists from the prefixes from another word, then the program simply changes the "End of Word" variable to "True".

For example, imagine an empty Trie containing only the root node. Then insert the word key "There". After that, insert "Then". What happens is at the third letter, 'e', the program creates a new node pointing to 'n' and sets that node as the "End of Word". If you insert "The" after that, the third letter 'e' also becomes an "End of Word".

Tries - Searching

----------------------------------------------------------------------

Searching for a key has the program compare the letters from the key with the Trie, from the root and move down from there. The search function can terminate if it exceeds the length of the key, if the string ends, or if there lacks the key letter in the Trie. If one of the first two conditions are met, and the last letter has a "True" for its End of Word value, then the key is present within the Trie. Otherwise, the key doesn't exist within the Trie.

Closing

----------------------------------------------------------------------

Thank you for having read this article to the end. I hope this can help you!

References:
https://www.geeksforgeeks.org/heap-data-structure/
https://www.cprogramming.com/tutorial/computersciencetheory/heap.html
https://www.tutorialspoint.com/min-max-heaps
https://www.geeksforgeeks.org/trie-insert-and-search/
https://medium.com/basecs/trying-to-understand-tries-3ec6bede0014
https://www.hackerearth.com/practice/data-structures/advanced-data-structures/trie-keyword-tree/tutorial/
http://www.mathcs.emory.edu/~cheung/Courses/323/Syllabus/Text/trie01.html

AVL Tree

Introduction to AVL Tree

----------------------------------------------------------------------

AVL Tree is a variation of Binary Search Tree that performs self-balancing so that the height difference between the right and left subtrees is no more than one. The advantage of having a balanced Binary Tree is having a better worst-case search speed compared to a regular Binary Search Tree. AVL Tree guarantees that the search speed will always be at O(log n).

Example of what constitutes as an AVL Tree, and what doesn't:

In AVL Trees, Balance Factor refers to the height difference between the right and left subtrees. An AVL Tree may have a Balance Factor of 1, -1, or 0 to be acknowledged as an AVL Tree.

Insertion

----------------------------------------------------------------------

AVL Trees has an insertion operation like normal Binary Search Trees. However, AVL Tree checks whether the balance factor of the tree is 1, -1, or 0. If not, then it will perform rebalancing. There are four main ways to rebalance a tree, known as Left Rotation, Right Rotation, Left-Right Rotation, or Right-Left Rotation.

Insertion - Single Rotation

----------------------------------------------------------------------

Single Rotation is a term that refers to Left Rotation and Right Rotation. It means that rebalancing the tree will only take one rotation. Left Rotation is used when the imbalance is in the left subtree, and Right Rotation is used when the imbalance is in the right subtree. Single Rotation is performed when the opposing subtree follows a straight path (left-left or right-right)

Examples of Left and Right Rotation:

Insertion - Double Rotation

----------------------------------------------------------------------

Double Rotation is a term that refers to Left-Right Rotation and Right-Left Rotation. Double Rotation is performed when the imbalance requires two rotations to be fixed. Double Rotation is performed when the opposing subtree has a zig-zag shaped path (left-right path or right-left path).

Left-Right Rotation occurs when the problem is in the right subtree of the left subtree, like so:
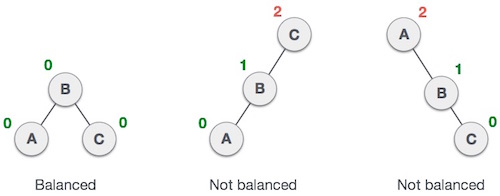
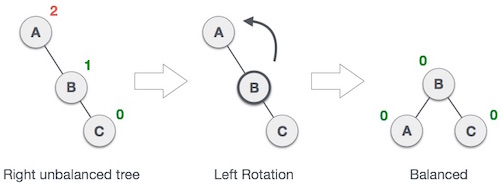
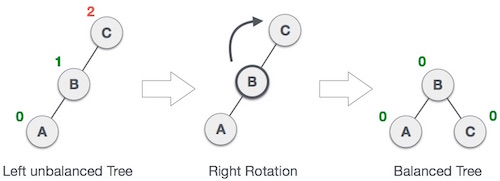
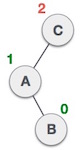 (From C, it goes a left->right path towards B)

On the other hand, Right-Left Rotation occurs when the problem is in the left subtree of the right subtree, like so:
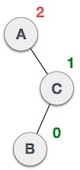 (From A, it goes a right->left path towards B)

A Double Rotation problem can be visualized as such:

What happens in both cases is that single rotation occurs two times on the "pivot".

Deletion

----------------------------------------------------------------------

Like with Insertion, Deletion in AVL Tree is just like Deletion in a regular Binary Search Tree, and then it checks if the tree has any imbalance on it. If the balance factor after deleting a node is not 1, -1 or 0, then it will perform one of the four rotations. The main difference with AVL Tree Insertion is that after performing a rotation, it will continue to check whether an imbalance has occured on the ancestors of the rotated node.

Example of AVL Tree Deletion:

Closing

----------------------------------------------------------------------

Thanks for having read this article to the end!

References:
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm
https://www.w3schools.in/data-structures-tutorial/avl-trees/