Hash Table and Binary Tree

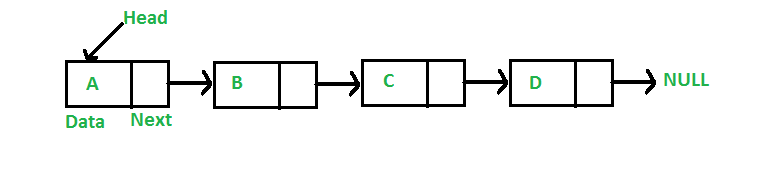
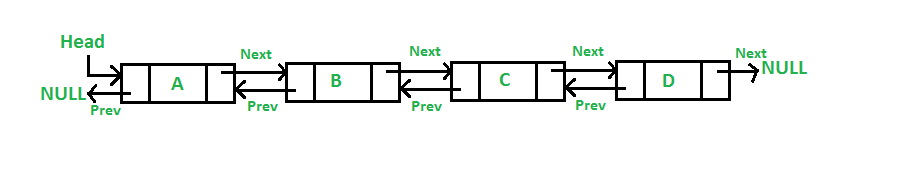
Introduction to Hash Table

----------------------------------------------------------------------

Hashing is a part of Data Structure that maps certain values with keys. These keys are shorter and easier to read than the value itself, so it is used to increase efficiency when referring to a value. How much more efficient it becomes will depend on the type of hashing that is used. A Hash Table is an array where the hash keys are stored. The method used to create the Hash Table is called Hash Function.

Example of Hash Table:

Wherein List contains the original values, H(x) is the Hash Function, and the array addresses are the keys.

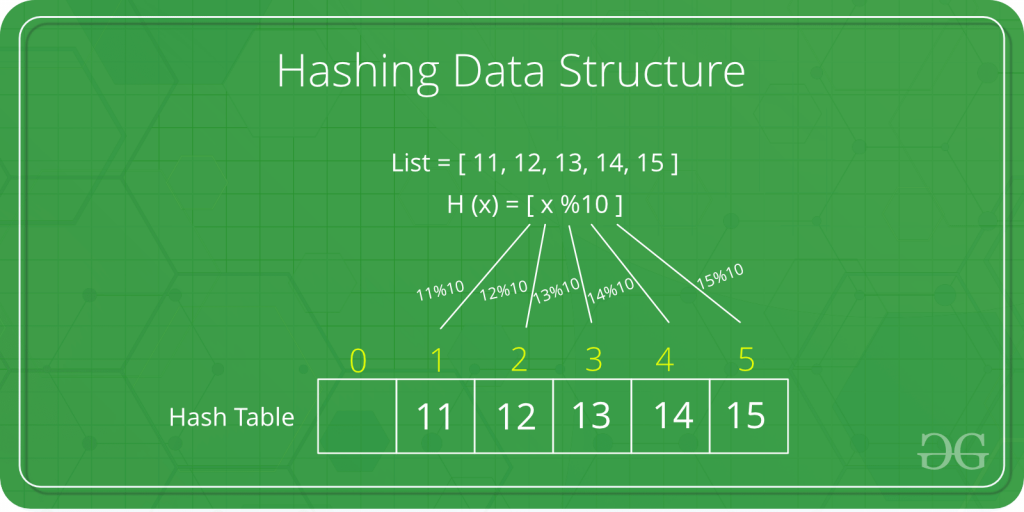
Hash Functions

----------------------------------------------------------------------

There are a very wide variety of Hash Functions, but on this article, I will only explain about Mid-square, Division, Folding, Digit Extraction and Rotating Hash.

Mid-square is a Hash Function where the value is squared, and then taking the middle part of the squared value as the key. For example, with a value of 2175, it will be squared to become 4730625. We take the middle part, which is 306, to become the key. In Mid-square, collision has a low probability of occurring, but still noticeable. An example is for values 2000 and 9000, both will result in a key of 000. It is also important to remember that squaring a value may cause overflow. If an overflow occurs, it can be fixed by using long long integer data type or using string as multiplication.

Division (or also known as Mod method) is a Hash Function where the key is Value % (modulus) Constant. For example, with a value of 64971 % 97, it will result in a key of 78. It is known that Division works best with a prime number as its modulus constant. The larger the prime number, the better. Collision can still occur with any constant, for example 472819 and 740166 has the same key value, being 38.

Folding is a Hash Function where the value is partitioned, then the parts are added to form the key. For example, with a value of 56143, the value is split into 56, 14 and 3, then added to become 73. Folding is relatively fast, and also prevents Collision quite well, but not completely. For example, 12356 and 48301 both has a key of 71.

Digit Extraction is a Hash Function where digits of the value is taken to create a shorter value as the key. For example, with a value of 3728192, we take the first, third, fifth and seventh value to form 3212 as the key. Collision can occur if the digits taken are the same. For example, the values 12345 and 18355 would have the same keys.

Rotating Hash is a Hash Function where a key from another Hash Function has its rightmost digit shifted onto the leftmost digit. For example, a key of 473 becomes 347 after Rotating Hash. Rotating hash helps with preventing Collisions.

Collision Handling

----------------------------------------------------------------------

In Hashing, there is a very real possibility that Hash Functions has certain values with the same keys. This is called Collision. There are two ways to handle a collision, those being Chaining and Open Addressing.

Chaining makes use of Linked Lists so that when a Collision occurs, the key for that value will be stored in the next node. This has the disadvantage of using larger amounts of memory, and is more suitable for larger programs.

Open Addressing or Linear Probing is when a Collision occurs, the key for a certain value will change by a certain amount, such as +1, until a Collision no longer occurs. This has the disadvantage of potentially making the Hash Table hard to read.

Introduction to Tree

----------------------------------------------------------------------

A Tree is a hierarchial Data Structure, which allows for faster and easier access. There are a number of terminologies that are used for Trees, the most basic of them being Node and Edge. Values are contained by Nodes and Nodes are connected by Edges. Here is an example of a Tree:

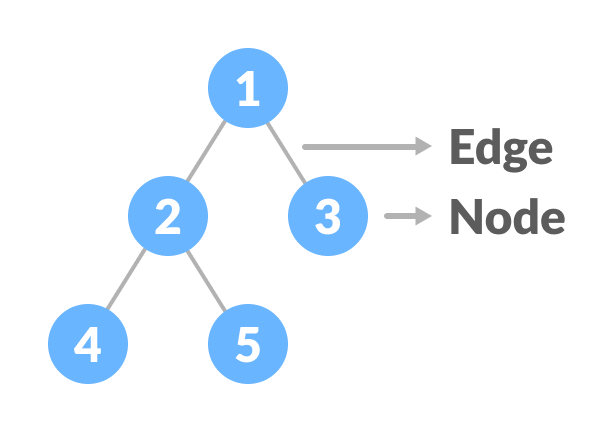
Other than those, Root describes the topmost Node of a Tree, a Child is a Node that branches from another Node, a Leaf is a Node that doesn't have any child and a Forest is a set of disjointed trees. A Node has Height/Depth and Degree. Height/Depth describes the number of edges towards/from the deepest leaf. The Height/Depth for a Root Node is also the Height/Depth for the Tree. Degree describes the number of branches in the Node.

Binary Tree

----------------------------------------------------------------------

Binary Tree is a Tree where each Node has a maximum of two Children. Each Node contains a data, a left pointer and a right pointer. In C, it would look like this:

struct node {
int data;
struct node *left;
struct node *right;
};

In a Binary Tree, it is possible to count the maximum possible amount of Nodes at the level "l" with the formula 2l-1 and the maximum possible amount of  Nodes at height "h" with 2h – 1.

Types of Binary Trees

----------------------------------------------------------------------

Binary Trees have multiple variations, the most common of them being Perfect, Complete, Skewed and Balanced Binary Trees.

Perfect Binary Tree or Full Binary Tree is a Binary Tree where every node except for the leaves has two children. In a Perfect Binary Tree, you can count the amount of leaves by adding the number of Nodes before it + 1.

Complete Binary Tree is a Binary Tree where every level of the tree, except for maybe the last level, has the maximum amount of Nodes. A Perfect Binary Tree is always also a Complete Binary Tree.

Skewed Binary Tree or Degenerate Binary Tree is a Binary Tree where every Node has at maximum one child.

Balanced Binary Tree is a Binary Tree where none of the leaves are shorter or further than any other leaves from the root.

Expression Tree is a Binary Tree where every leaf contains an operand and every other node contains an operator. Expression Trees can be used for Prefix, Postfix and Infix Traversals.

Threaded Binary Tree is a Binary Tree variant where Node pointers previously pointing towards NULL, now points to a previous Node.

References:
https://www.geeksforgeeks.org/hashing-data-structure/
https://www.geeksforgeeks.org/mid-square-hashing/
https://www.baeldung.com/folding-hashing-technique
http://blog4preps.blogspot.com/2011/07/hashing-methods.html
https://eternallyconfuzzled.com/hashing-c-introduction-to-hashing
https://www.programiz.com/dsa/trees
https://www.geeksforgeeks.org/binary-tree-data-structure/
https://www.geeksforgeeks.org/threaded-binary-tree/
https://greatnusa.com/theme/trema/view.php?id=178

Introduction to Linked Lists

Introduction to Linked List

----------------------------------------------------------------------

Linked List is one of the many types of Data Structure. In a Linked List, each data record is accompanied with a reference to the next data record, and in certain variations, a reference to the previous data record. A Linked List has the advantage of being able to insert and delete any data record from any location. This makes a Linked List suitable for real-time programs where the amount of data is hard to predict and for programs that require accessing the data records sequentially. However, Linked Lists makes it hard to search for a specific data, as it doesn't allow for random access and has to check each data one-by-one sequentially. It also takes up a large amount of memory.

A Linked List are based around the usage of 'Nodes', which contains a data record and an address pointing to the next node. Some Linked Lists also have an additional address, pointing to the previous node. To determine which Node the program will add a data record to, Linked Lists makes use of a 'Head' address. The Head address usually begins at the first Node before moving to other Nodes. At the end of a Linked List is a 'Null' address to indicate that the Linked List has ended.

Types of Linked List

----------------------------------------------------------------------

Linked Lists have multiple variations, the most popular of them include:

- Singly Linked List

Singly Linked List is the most basic form of a Linked List, and contains only the minimum of what a Linked List has. Within the node, there only exists an address to the next node.

This is how a Singly Linked List node looks like in C:

struct Node { 

int data; 

struct Node* next; 

}; 

Visual example of a Singly Linked List:

- Circular Linked List

Circular Linked List is virtually the same as with a Singly Linked List, but at the end of the Linked List, the Null address is replaced by an address that points to the first Node. This type of Linked List can be used if the program has to cycle through the List multiple times.

Visual example of a Circular Linked List:

- Doubly Linked List

In a Doubly Linked List, the Node does not only contain an address for the next Node, but also an address pointing to the previous Node. This makes it faster to insert and delete Nodes that are located in the middle, but also uses more memory than a Singly Linked List.

This is how a Doubly Linked List node looks like in C:

struct Node { int data; struct Node* next; // Pointer to next node in DLL struct Node* prev; // Pointer to previous node in DLL };

Visual example of a Doubly Linked List:

- Circular Doubly Linked List

Circular Doubly Linked List combines the features of Circular and Doubly Linked List along with the inherent advantages that comes with it, but has the obvious drawback of taking up more memory.

Visual example of a Doubly Linked List:

Insertion and Deletion

----------------------------------------------------------------------

One of the main advantages that a Linked List has to offer is that it can insert and delete Nodes from any location. To better explain this advantage point, we will look at snippets of how insertion and deletion can be done in Singly Linked Lists. These snippets are taken from geeksforgeeks.org

In Linked Lists, insertion is done by allocating the memory for a new Node, putting in the data into the Node and then placing the Node in the required position. Linked List insertion has three main variants, insertion from the front, in the middle, and at the end of the List.

We will begin with insertion from the front. In C, this would look like:

void push(struct Node** head_ref, int new_data) 

{ 

/* 1. allocate node */

struct Node* new_node = (struct Node*) malloc(sizeof(struct Node)); 

/* 2. put in the data */

new_node->data = new_data; 

/* 3. Make next of new node as head */

new_node->next = (*head_ref); 

/* 4. move the head to point to the new node */

(*head_ref) = new_node; 

} 

Now, let us compare with insertion in the middle of the Linked List and at the end of the Linked List. In C, inserting between two Nodes would look like:

void insertAfter(struct Node* prev_node, int new_data) 

{ 

/*1. check if the given prev_node is NULL */

if (prev_node == NULL) 

{ 

printf("the given previous node cannot be NULL");  

return; 

} 

/* 2. allocate new node */

struct Node* new_node =(struct Node*) malloc(sizeof(struct Node)); 

/* 3. put in the data */

new_node->data = new_data; 

/* 4. Make next of new node as next of prev_node */

new_node->next = prev_node->next; 

/* 5. move the next of prev_node as new_node */

prev_node->next = new_node; 

} 

The main difference between the two is that when inserting in the middle, the program has to check whether the query given for where the new Node would be is Null or not. Other than that, these two are the same.

As for insertion at the end of the List, in C it would look like:

void append(struct Node** head_ref, int new_data) 

{ 

/* 1. allocate node */

struct Node* new_node = (struct Node*) malloc(sizeof(struct Node)); 

struct Node *last = *head_ref; /* used in step 5*/

/* 2. put in the data */

new_node->data = new_data; 

/* 3. This new node is going to be the last node, so make next 

of it as NULL*/

new_node->next = NULL; 

/* 4. If the Linked List is empty, then make the new node as head */

if (*head_ref == NULL) 

{ 

*head_ref = new_node; 

return; 

} 

/* 5. Else traverse till the last node */

while (last->next != NULL) 

last = last->next; 

/* 6. Change the next of last node */

last->next = new_node; 

return;  

} 

There are a few differences between inserting from the front and at the end. The first is that instead of pointing to the next Node, it instead points at Null. The second is that it has to first search for the last Node before inserting. Step 4 is only there to prevent an error; if this function is used anytime after using the push function, it is not required.

Linked List deletion is done by first searching for the Node that it will delete, unlink the Node and finally free the memory allocation. As for deletion, there are two variations; deleting a Node by its value or by the Node's position. In C, this code can be used to delete a Node by a key value

void deleteNode(struct Node **head_ref, int key)
{
// Store head node
struct Node* temp = *head_ref, *prev;

// If head node itself holds the key to be deleted
if (temp != NULL && temp->data == key)
{
*head_ref = temp->next; // Changed head
free(temp); // free old head
return;
}

// Search for the key to be deleted, keep track of the
// previous node as we need to change 'prev->next'
while (temp != NULL && temp->data != key)
{
prev = temp;
temp = temp->next;
}

// If key was not present in linked list
if (temp == NULL) return;

// Unlink the node from linked list
prev->next = temp->next;

free(temp); // Free memory
}

In comparison, here is what deleting by a Node's position looks like in C:

void deleteNode(struct Node **head_ref, int position)
{
// If linked list is empty
if (*head_ref == NULL)
return;

// Store head node
struct Node* temp = *head_ref;

// If head needs to be removed
if (position == 0)
{
*head_ref = temp->next; // Change head
free(temp); // free old head
return;
}

// Find previous node of the node to be deleted
for (int i=0; temp!=NULL && i<position-1; i++)
temp = temp->next;

// If position is more than number of ndoes
if (temp == NULL || temp->next == NULL)
return;

// Node temp->next is the node to be deleted
// Store pointer to the next of node to be deleted
struct Node *next = temp->next->next;

// Unlink the node from linked list
free(temp->next); // Free memory

temp->next = next; // Unlink the deleted node from list
}

As can be seen, there are not many differences between the two. The biggest difference is in what the code is searching for; a key value or a specific Node.

Closing

----------------------------------------------------------------------

For examples of what a simple, completed program with Linked List looks like, I recommend you to check out the referenced links at the bottom of this post. There are more dedicated sites for educational purposes, and I think having them here will cause the post to go for too long. Regardless, thank you for having spent your time reading this post. I hope that you can help me with my future writing by giving me suggestions for posts like this.

Reference:

https://www.geeksforgeeks.org/data-structures/linked-list/

https://www.programiz.com/dsa/linked-list

Welcome to my blog!

This is the first blog I've created, originally made for my assignments. However, as time goes on, I imagine the content will become more varied and personalized.

Anyway, thank you for visiting, and I hope you'll enjoy your stay here.